事业单位考试行测复习4

>>事业单位考试行测复习：事业单位考试行测复习4

>>事故单位笔试钻石课程

容斥问题

先通过一道简单的例题来认识一下容斥问题：

例1.某班共有50人，有30人喜欢绘画，35人喜欢音乐，1人两种都不喜欢，问同时喜欢绘画和音乐的有多少人?

在这道题目里面我们发个数据间有重复，为了使统计的数目无一重复，无一遗漏，我们先不考虑重复的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。而具体做题时，往往要将容斥原理和文氏图结合起来使用，所以上面的题目我们可以用图解法求解。

【解析】：设同时喜欢音乐和绘画的有X人：

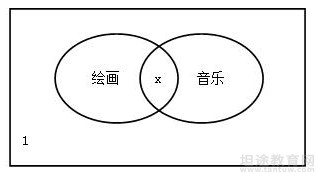
可列式30+35-X+1=50可得X=16人。

例2.工厂组织职工参加周末公益劳动，有80%的职工报名参加。其中报名参加周六活动的人数与报名参加周日活动的人数比为2∶1，两天的活动都报名参加的人数为只报名参加周日活动的人数的50%。问未报名参加活动的人数是只报名参加周六活动的人数的：

A.20% B.30%

C.40% D.50%

【解析】：由题意可做图形：

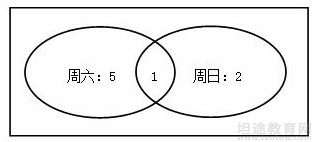
并且设周六周日都参加的为1人。则可得只参加周日为2人，只参加周六为5人。参加的人为8人。那么未参加的为2人。所以没参加的人为只参加周六的：2÷5=40%。

这类容斥问题考法也很固定，无论是两者容斥或者三者容斥我们的解题原则就是让重叠的部分变为一层。

而容斥问题还有一类为容斥极值问题，利用基本计算公式求几个集合交集的最小值就等于：A+B+C-2I。(其中I为全集)。A,B,C,D四个集合的交集的最小值就等于：A+B+C+D-3I(其中I为全集)。

例如：.某数学竞赛共160人进入决赛，决赛共4题，做对第一题的有136人，做对第二题的有125人，做对第三题的有118人，做对第四题的有104人。那么，在这次决赛中至少有几人得满分?

A.3 B.4 C.5 D.6

利用公式就得所求为：136+125+118+104-160×3=3。

登录坦途网事业单位考试频道，为你提供2017年事业编制考试行政能力测验综合辅导，让你获得更多事业编制考试行测答题技巧，让你的备考更加有效。