2018造价工程师《案例分析》习题及答案9

>>造价工程师案例分析：2018造价工程师《案例分析》习题及答案9

>>造价工程师名师推荐课程

背景：

某企业生产的某种产品在市场上供不应求，因此该企业决定投资扩建新厂。据研究分析，该产品10年后将升级换代，目前的主要竞争对手也可能扩大生产规模，故提出以下三个扩建方案：

1.大规模扩建新厂，需投资3亿元。据估计，该产品销路好时，每年的净现金流量为9000万元;销路差时，每年的净现金流量为3000万元。

2.小规模扩建新厂，需投资1.4亿元。据估计，该产品销路好时，每年的净现金流量为4000万元;销路差时，每年的净现金流量为3000万元。

3.先小规模扩建新厂，3年后，若该产品销路好再决定是否再次扩建。若再次扩建，需投资2亿元，其生产能力与方案1相同。

据预测，在今后10年内，该产品销路好的概率为0.7，销路差的概率为0.3。

基准收益率ic =10%，不考虑建设期所持续的时间。

表2-24 现值系数表

问题：

1.画出决策树。

2.试决定采用哪个方案扩建。

分析要点：

本案例已知三个方案的净现金流量和概率，可采用决策树方法进行分析决策。由于方案3需分为前3年和后7年两个阶段考虑，因而本案例是一个两级决策问题，相应地，在决策树中有两个决策点，这是在画决策树时需注意的。另外，由于净现金流量和投资发生在不同时间，故首先需要将净现金流量折算成现值，然后再进行期望值的计算。

本案例的难点在于方案3期望值的计算。在解题时需注意以下几点：

一是方案3决策点Ⅱ之后的方案枝没有概率枝，或者说，销路好的概率为1.00但是，不能由此推论两级决策点后的方案枝肯定没有概率枝。

二是背景资料未直接给出方案3在三种情况下(销路好再次扩建、销路好不扩建、销路差)的净现金流量，需根据具体情况，分别采用方案1和方案2的相应数据。尤其是背景资料中的“其生产能力与方案1相同”，隐示其年净现金流量为9000万元。

三是机会点③期望值的计算比较复杂，包括以下两种状态下的两个方案：(1)销路好状态下的前3年小规模扩建，后7年再次扩建; (2)销路差状态下小规模扩建持续10年。

四是需二次折现，即后7年的净现金流量按年金现值计算后，还要按一次支付现值系数折现到前3年年初。

答案：

问题1：

解：根据背景资料所给出的条件画出决策树，标明各方案的概率和净现金流量，如图2-2所示。

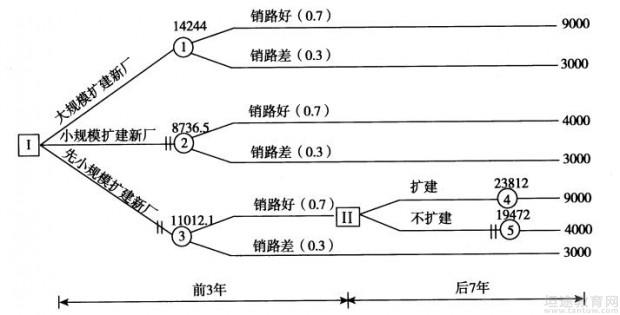
图2—2 决策树

问题2：

解：1.计算二级决策点各备选方案的期望值并做出决策机会点④的期望值：9000×(P/A,IO%，7)-20000=9000×4.868一删=23812(万元)机会点⑤的期望值：4000×(P/A，10%，7)= 4000×4.868=19472(万元)

由于机会点④的期望值大于机会点⑤的期望值，因此应采用3年后销路好时再次扩建，的方案。

2.计算一级决策点各备选方案的期望值并做出决策

机会点①的期望值：(9000×0.7+3000×0.3)×(P/A，10% ,10)-30000 = 7200×6.145 - 30000=14244(万元)

机会点②的期望值：(4000×0.7+3000×0.3)×(P/A,lO% ,10)-14000= 3700×6.145 - 14000=8736.5(万元)

机会点③的期望值：

4000×0.7×(P/A，10% ,3)+23812 ×O.7×(P/F,IO% ,3)+3000 ×O.3×(P/A,10%,10) - 14000=4000×0.7×2.487+23812×0.7×0.751+3000×0.3×6.145-14000- 11012.1(万元)

由于机会点①的期望值最大，故应采用大规模扩建新厂方案。

不管你是否决定参加2018年造价工程师考试，小编在此诚挚的邀请你进入坦途网造价工程师考试频道，更多精彩总结让你一步了解造价工程师，全面备考！