2018造价工程师《案例分析》习题及答案8

>>造价工程师案例分析：2018造价工程师《案例分析》习题及答案8

>>造价工程师名师讲解课程

背景：

某建设项目有A、B、C三个投资方案。其中，A方案投资额为2000万元的概率为0.6，投资额为2500万元的概率为0.4;在这两种投资额情况下，年净收益额为400万元的概率为0.7，年净收益额为500万元的概率为0.30

通过对B方案和C方案的投资额数额及发生概率、年净收益额数额及发生概率的分析，得到该两方案的投资效果、发生概率及相应的净现值数据，见表2-23。

表2-23 B方案和C方案评价参数表

假定A、B、C三个投资方案的建设投资均发生在期初，年净收益额均发生在各年的年末，寿命期均为1 0年，基准折现率为10%。

在计算净现值时取年金现值系数(P/A，1 0%，10) =6.1450

问题：

1.简述决策树的概念。

2.A方案投资额与年净收益额四种组合情况的概率分别为多少?

3.A方案净现值的期望值为多少?

4.试运用决策树法进行投资方案决策。

分析要点：

本案例考核决策树法的运用，主要考核决策树的概念及其绘制和计算，要求熟悉决策树法的适用条件，能根据给定条件正确画出决策树，并能正确计算各机会点的数值，进而做出决策。

决策树的绘制是自左向右(决策点和机会点的编号左小右大，上小下大)，而计算则是自右向左。各机会点的期望值计算结果应标在该机会点上方，最后将决策方案以外的方案枝用两短线排除。

需要说明的是，在题目限定用决策树法进行方案决策时，要计算各方案投资额与年净收益四种组合情况的概率及相应的净现值，进而计算各方案净现值的期望值。但是，如果题目仅仅要求计算各方案净现值的期望值，则可以直接用年净收益额的期望值减去投资额的期望值求得净现值的期望值。为此，问题3给出了两种解法。

答案：

问题1：

答：决策树是以方框和圆圈为节点，并由直线连接而成的一种像树枝形状的结构，其中，方框表示决策点，圆圈表示机会点;从决策点画出的每条直线代表一个方案，叫作方案枝，从机会点画出的每条直线代表一种自然状态，叫作概率枝。

问题2：

解：

投资额为2000万元与年净收益为400万元组合的概率为：0.6×0.7=0. 42

投资额为2000万元与年净收益为500万元组合的概率为：0.6×0.3=0.18

投资额为2500万元与年净收益为400万元组合的概率为：0.4×0.7=0.28

投资额为2500万元与年净收益为500万元组合的概率为：0.4×0.3=0.12

问题3：

解1：

投资额为2000万元与年净收益为400万元组合的净现值为：

NPV1=- 2000+400×6.145=458(万元)

投资额为2000万元与年净收益为500万元组合的净现值为：

NPV2 = - 2000+500×6.145=1072.5(万元)

投资额为2500万元与年净收益为400万元组合的净现值为：

NPV3=-2500+400×6.145=-42(万元)

投资额为2500万元与年净收益为500万元组合的净现值为：

NPV4=- 2500+500×6.145=572.5(万元)

因此，A方案净现值的期望值为：

E(NPVA) =458×0.42+1072.5×0.18 -42×0.28 +572.5×0.12 =442. 35(万元)

解2：

E(NPVA)=- (2000×0.6+2500×0.4)+(400×0.7+500×0.3)×6. 145= 442. 35(万元)

问题4：

解：1.画出决策树，标明各方案的概率和相应的净现值，如图2-1所示。

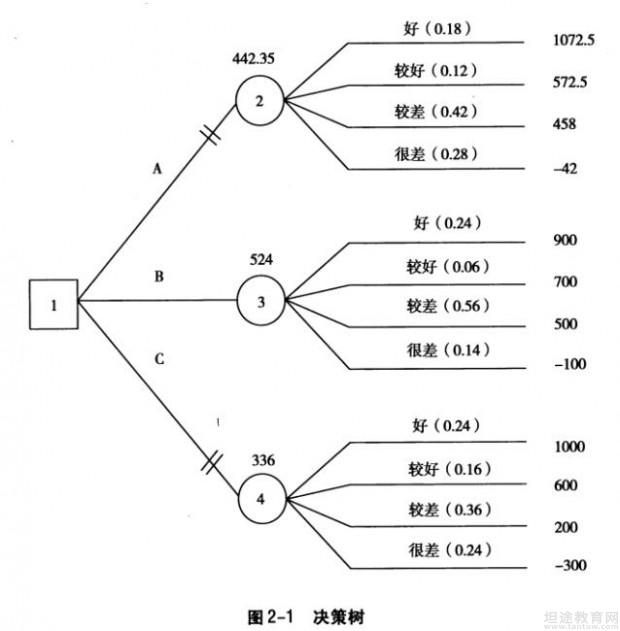
2.计算图2-1中各机会点净现值的期望值(将计算结果标在各机会点上方)o

机会点②：E(NPVA)=442. 35(万元)(直接用问题3的计算结果)

机会点③：E(NPVB) =900×0.24 +700×0. 06 +500×0.56- 100×0. 14 =524(万元)

机会点④：E(NPVc)=1000×0. 24 +600×0. 16 +200×0. 36 -300×0. 24 =336(万元)

3.选择最优方案。

因为机会点③净现值的期望值最大，故应选择B方案。

计划参加2018年造价工程师考试的考生赶快看向这里，坦途网造价工程师考试频道已经为大家准备好2018造价工程师《案例分析》习题及答案。最后，小编祝大家考试顺利，成功完成目标！